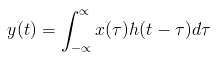TIme-shifting a signal

time-shifting a signal

band-limited σήματα

Αν μας δίνεται ένα αναλογικό σήμα και μας ρωτάει αν είναι band-limited(περιορισμένου εύρους) τότε εμείς θα πρέπει να βρούμε τον μετασχηματισμό Fourier του σήματος,δηλαδή αν μεταφερθούμε στο πεδίο των συχνοτήτων, και να δούμε αν αυτός μηδενίζεται πάνω από μια ορισμένη συχνότητα.Αν αυτό συμβαίνει τότε το σήμα μας είναι band-limtied.

παράδειγμα

ΕΠΑΝΑΛΗΨΗ

Άσκηση 2.2(a) ok
Άσκηση 2.2(b) ok


Λυμένες Ασκήσεις
4ο σετ
άσκηση 1
άσκηση 2 
άσκηση 3 **  Ο ML αναφέρεαται σε συνεχή χρόνο άρα έχω ολοκλήρωμα
άσκηση 4      Προσοχή όταν ανεβάζω j από παρονομαστή σε αριθμητή
άσκηση 5 εύκολη

3ο σετ
άσκηση 1 (απόδειξη περιοδικότητας ενός σήματος, καλή)!
άσκηση 2  περιοδικά σήματα διακριτού χρόνου
άσκηση 3 παράξενη
άσκηση 4 εύκολη

Σεπτέμβριος 2011
ΙΙe) Βαθμός δυσκολίας 5
ΙΙb) πράξεις δυσκολία 4
Ia) σχετικά εύκολο δυσκολιά 3

ΠΡΟΣΟΧΗ (άσκηση 3 από πρόοδο)
-Συνέλιξη στο πεδίο του χρόνου πολλαπλασιασμός στο πεδίο της συχνότητας
ΑΛΛΑ ΚΑΙ
-Πολλαπλασιασμός στο πεδίο του χρόνου συνέλιξη στο πεδίο της συχνότητας  επί 1/(2pi)

να δω σήματα ενέργειας
να δω σειρά fourier 1o set

συνέλιξη στον διακριτό χρόνο [πρόοδος][ομάδα Α][θέμα 2]

DFT

Περιοδικότητα σημάτων

• [1ο σετ λυμένων ασκήσεων][άσκηση 4]  
• [1ο σύνολο ασκήσεων][άσκηση 1.1.b] sos iv

διαφορική εξίσωση με ΜL

• [3ο σύνολο ασκήσεων][άσκηση 3.2]
• προσοχή στην ευστάθεια και αν υπάρχει η  απόκριση συχνότητας

θεώρημα δειγματοληψίας Shannon

• σύμφωνα με το θεώρημα δειγματοληψίας του Shannon, ο ρυθμός δειγματοληψίας πρέπει να ξεπερνάει τον όρο Nyquist, δηλαδή ισοδύναμα Ωmax<π/Ts
• Η μέγιστη συχνότητα του σήματος καλείται και bandwidth.

EXL:
Υποθέστε ότι έχουμε δύο ζωνοπερατά(bandlimited) σήματα x1(t) και x2(t) για τα οποία ισχύει X1(Ω)=0 για |Ω|>500π και X2(Ω)=0 για |Ω|>1000π.Ποιά είναι η μέγιστη περίοδος δειγματοληψίας Ts, ώστε να μπορούν να κατασκευασθούν τα δείγματά τους;
i. x1(t)
SOL
Επειδή το σήμα x1 μηδενίζεται για συχνότητες μεγαλύτερες του 500π παίρνουμε ότι το bandwidth του σήματος είναι 500π.Από το θεώρημα του Nyquist γνωρίζουμε ότι η συχνότητα δειγματοληψίας πρέπει να είναι διπλάσια από το bandwidth του σήματος άρα Ωs=1000π. Μην ξεχνάμε ότι Ωs=2π/Τs από που και μπορούμε να βρούμε την περίοδο δειγματοληψίας.

1. Συνέλιξη δύο σημάτων στο χρόνο έχουμε πολλαπλασιασμό στο πεδίο της συχνότητας άρα το bandwidth είναι το ελάχιστο των δύο bandwidth.
2. Πρόσθεση δύο σημάτων στο πεδίο του χρόνου έχουμε πρόσθεση και στο πεδίο της συχνότητας άρα το μέγιστο bandwidth είναι το μέγιστο bandwidth των δύο σημάτων.
3. Πολλαπλασιασμό των δύο σημάτων στο πεδίο του χρόνου έχω συνέλιξη στο πεδίο της συχνότητας άρα το μέγιστο bandwidth του σήματος είναι το άθροισμα των bandwidth των δύο σημάτων.

Μέτρο μιγαδικού αριθμού

το μέτρο του μιγαδικού αριθμού είναι το πραγματικό μέρος υψωμένο στο τετράγωνο συν το πραγματικό μέρος υψωμένο στο τετράγωνο και όλο αυτό σε ρίζα.

z-transform of a sequence [EXL]

http://youtu.be/i2_8p_N8urs?t=6m12s

Poles

The real part of the pole :

•  > 0  determines whether something grows exponentially
• = 0 ,stays constant
• < 0 ,decreases exponentially

The imaginary part of the pole tells me whether there is an isolation in a time signal.

Αντίστροφα συστήματα

Πότε ένα σύστημα δεν είναι αντιστρέψιμο;
όταν διαφορετικοί είσοδοι μπορούν να οδηγήσουν σε διαφορετική έξοδο.

παράδειγμα:
έχω ένα σύστημα y(t)=x(t-2) και θέλω να βρω το αντίστροφό του.Παρατηρώ ότι αυτό που κάνει το σύστημα είναι να ολισθαίνει το σήμα εισόδου κατά 2 μονάδες αριστερά άρα θα πρέπει να βρω ένα σήμα που να το ολισθαίνει κατά 2 μονάδες δεξιά.Το σύστημα που κάνει αυτή την δουλειά είναι το z(t)=x(t+2)

Πρόοδος

• συνέλιξη στον διακριτό χρόνο(ok, αλλά να δω και την άσκηση με το πινακάκι)
• αντίστροφος M.F. με μερικά κλάσματα(ok, αλλά να το ξαναδώ)

1. δεν έβαλε σειρά Fourier
2. δεν έβαλε συνέλιξη σε διακριτό χρόνο

Rational numbers

click

Discrete time convolution

N->Index of the first non-zero value of x[n]
M->Index of the first non-zero value of h[n]

Then write an array

• y[n] = 0 for n < N+M
  

Ολοκλήρωση κατά παράγοντες

noisi.net

Αιτιατό - Μη αιτιατό

• Ένα σύστημα λέγεται αιτιατό όταν το σήμα εξόδου,y(t), εξαρτάται από τις τιμές του σήματος εισόδου στην παρούσα,t, και προηγούμενες χρονικές στιγμές.
• Αν η έξοδος του συστήματος εξαρτάται και από μελλοντικές τιμές της εισόδου, το σύστημα καλείται μη-αιτιατό.

EXL:

1. y(t)=x(t)x(t-2) Η έξοδος εξαρτάται από την τιμή της εισόδου τώρα x(t) και στο παρελθόν x(t-2) άρα το σύστημα είναι αιτιατό.

ps:αν μας δίνει την κρουστική απόκριση και το σήμα εισόδου και μας ρωτάει αν το σύστημα είναι αιτιατό εμείς θα κοιτάμει πάντα την κρουστική απόκριση(h[n]) διότι όπως γνωρίζουμε ένα σύστημα περιγράφεται πλήρως από την κρουστική του απόκριση.

Memoryless and NOT Memoryless systems

Memoryless system is the system that doesn't require memory

EXL:
y(t) = 5*x(t) MEMORYLESS
y(t)=2*x(t-7) NOT MEMORYLESS
y(t)=6*x(t/8) NOT MEMORYLESS

Find Period Of Two Signals

• If both periods (T1 & T2) are integers find the least common multiple
  EXL:
  T1=4 & T2=6 OVERALL PERIOD=LCM(4,6)=12
• If T1 & T2 are fractions do:
• find the lcm of denominators(lcmd)
• multiply x=lcmd*T1 & y=lcmd*T2
• find the lcm(x,y)
• divide by lcmd

source

ROC

Η περιοχή σύγκλισης του μετασχηματισμού Laplace μιας συνάρτησης δεν περιλαμβάνει πόλους.


Η περιοχή σύγκλισης του μετασχηματισμού Ζ για αιτιατό σήμα εκτείνεται έξω από έναν κύκλο με κέντρο 0 και ακτίνα r_ στο επίπεδο των z.

Συνάρτηση μεταφοράς και κύκλωμα

Σε ένα σύστημα για να βρούμε την συνάρτηση μεταφοράς, θεωρούμε όλες τις αρχικές συνθήκες μηδέν.

Ευστάθεια στον ΜL

Εάν πόλοι της συνάρτησης μεταφοράς ενός αιτιατού συστήματος βρίσκονται στο δεξιό μιγαδικό ημιεπίπεδο ή στον φανταστικό άξονα, τότε το σύστημα είναι ασταθές. Εάν όλοι οι πόλοι της συνάρτησης μεταφοράς βρίσκονται στο αριστερό μιγαδικό ημιεπίπεδο, τότε το σύστημα είναι ευσταθές.


Ορισμός ευστάθειας τύπου ΦΕΦΕ ενός αιτιατού ΓΧΑ συτήματος είναι ότι:
όλοι οι πόλοι της συνάρτησης μεταφοράς του πρέπει να έχουν αρνητικό πραγματικό μέρος.

Τα παραπάνω ισχύουν για αιτιατά σήματα.
Στην περίπτωση που το σύστημα δεν είναι αιτιατό, η συνάρτηση μεταφοράς του μπορεί να έχει πόλους και στο δεξιό ημιεπίπεδο.Η ΠΣ της H(s) θα πρέπει οπωσδήποτε πάλι να περιλαμβάνει τον φανταστικό άξονα.

Ευστάθεια στον ΜΖ

Για να είναι ένα σύστημα ταυτόχρονα ευσταθές και αιτιατό θα πρέπει όλοι οι πόλοι του να βρίσκονται εντός του μοναδιαίου κύκλου.

Laplace Domain Circuit

(right/left)-sided sequence

click

Ανάπτυξη σε Απλά Κλάσματα

click

e^(x) and e^(-x)

Μετασχηματισμός Laplace

Έχουμε δυνατότητα μετάβασης από τον Laplace στον Fourier όταν στο πεδίο σύγκλισης περιέχεται ο φανταστικός άξονας

Ασυνέχεια συνάρτησης και παράγωγος

Όταν μια συνάρτηση παρουσιάζει ασυνέχεια σε ένα σημείο, τότε ως παραγωγός της στο σημείο αυτό θα μπαίνει η δ(t) και μάλιστα πολλαπλασιασμένη με τον κατάλληλο αριθμό κάθε φορά.
Στην παρακάτω εικόνα απεικονίζεται η συνάρτηση:

και στην συνέχεια η παράγωγός της:

Orthogonality of Sines and Cosines

here

απόδειξη

ισχύει το παρακάτω:

οπότε:

διότι:
για τ > t όρισμα αρνητικό άρα η u μηδενίζεται
για τ <> όρισμα θετικό άρα η u ισούται με την μονάδα

Τριγωνομετρικές Συναρτήσεις

applet

Ορθοκανονικές Συναρτήσεις

παράδειγμα

Εσωτερικό γινόμενο

εδώ

Αιτιατή συνάρτηση (causal)

Ολίσθηση στην συχνότητα

Εάν

τότε


παρατηρήσεις:
Μπορεί να μας δώσουν ένα σήμα y(t) που περιέχει ένα σήμα x(t) με εκθετικό μπροστά.
Να βρω το Μετασχηματισμό Fourier του y(t) είναι πολύ εύκολο
αρκεί να ακολουθήσω την ιδιότητα της ολίσθησης στην συχνότητα.
Έτσι,
αρχικά θα βρω τον Μετασχηματισμό Fourier του x(t) και στην συνέχεια
θα το ολισθήσω κατά Ω0, όσο δηλαδή μου λέει το εκθετικό!

Χρονική ολίσθηση

Εάν

τότε

Γραμμικά και μη γραμμικά συστήματα

Θέλω να δω αν το σύστημα που η έξοδος του περιγράφεται από την παρακάτω εξίσωση είναι γραμμικό ή μη:

Γενικά θα είναι γραμμικό αν η απόκριση στο γραμμικό συνδυασμό δύο εισόδων ισούται με τον αντίστοιχο γραμμικό συνδυασμό των επιμέρους αποκρίσεων.
Αρχικά:

οπότε η έξοδος σε αυτό το γραμμικό συνδυασμό των δύο εισόδων είναι:

• 

Τώρα θα ελένξω τον αντίστοιχο γραμμικό συνδυασμό των επιμέρους αποκρίσεων:

• 

επειδή οι δυο αποκρίσεις διαφέρουν το σύστημα είναι μη γραμμικό!

Χρονικά αμετάβλητα και μεταβαλλόμενα συστήματα

Έχω το παρακάτω σήμα:

Θέλω να εξετάσω αν είναι χρονικά μεταβαλλόμενο.
Αρχικά παίρνουμε την είσοδο και την μετατοπίζουμε π.χ. κατά 3.Άρα:

οπότε η έξοδος γίνεται:

• 

Μετά κοιτάζω και την έξοδο μετατοπισμένη κατά 3.

• 

Αν τα δύο σήματα με την βούλα διαφέρουν(πράγμα που στο παράδειγμά μας αυτό συμβαίνει), τότε το σύστημα είναι χρονικά μεταβαλλόμενο.

Τί είναι η συνέλιξη;

Η συνέλιξη είναι το παρακάτω ολοκλήρωμα:

και γράφεται συμβολικά:

γραφική παράσταση πολυωνύμου

εδώ

Ιδιότητα παραγώγησης του Μετασχηματισμού Fourier

Τί είναι σύστημα;

Ως σύστημα έχουμε ορίσει τη διαδικασία που μετατρέπει μια φυσική ποσότητα, που περιγράφεται από το σήμα εισόδου,x(t), σε μια άλλη, που περιγράφεται από το σήμα
εξόδου, y(t)

σήμα εξόδου

έχω το σήμα εισόδου x(t), και γνωρίζω και πως συμπεριφέρεται το σύστημα
όταν ασκήσω πάνω του την κρουστική συνάρτηση ή συνάρτηση δέλτα.Με την
βοήθεια του ολοκληρώματος της συνέλιξης καιακολουθώντας την γνωστή διαδικασία
προκύπτει το σήμα εξόδου.

προσοχή στο παρακάτω ολοκλήρωμα

Θεώρημα Συνέλιξης

απορία σελ 43 βιβλίου

απάντηση

Γενικά:θα εξετάζω αν μια ολοκληρωτέα συνάρτηση είναι άρτια
ή περιττή ξεκινώντας πάντα από τον ορισμό.
ορισμός άρτιας
ορισμός περιττής
Ισχύουν τα γνωστά, ότι το συνημίτονο είναι μια άρτια συνάρτηση
και το ημίτονο μια περιττή συνάρτηση.
Το ολοκλήρωμα μια περιττής συνάρτησης απο το μειον άπειρο
έως το συν άπειρο είναι 0.

Dirac function

Γραφική παράσταση περιττής συνάρτησης

Ύλη Μαθήματος

από το βιβλίο
κεφ 1, κεφ 2, κεφ 3
κεφ 5 εκτος απο παραγράφους 5.4.4 , 5.5 ,5.7, 5.8(όλο εκτος), 5.9

Ιστοσελίδα Μαθήματος

εδώ